My mental model of wakes
...
All posts in this series:
1. Aerodynamics is beautiful and strange. Wakes especially so
2. A not-short-enough introduction to wakes and drag
3. Big wakes and small wakes
4. How should we think about shear layers?
5. My mental model of wakes
At this point, I've shared many of the interesting results and seeming conundrums that have influenced the way I think about vehicle wakes. I think aerodynamicists often misunderstand shear layers. I also think we have trouble conceptualizing whether we want the wake to be larger or smaller, and why. To wrap it all up, I'll try now to lay out my rough mental model of how wakes work.
Balance between shear and pressure
First, I think of wakes as a balance between shear forces (which generally pull air out of the wake) and fluid pressures (which draw air into the wake). I agree with Hoerner, for the reasons laid out in the previous essay, that we can think of a "jet pump" mechanism, where the high speed flow surrounding the wake pulls slow-moving air out of the wake.
I disagree with McLean that the jet pump is a myth—though I do agree with McLean that much about the wake is determined by the overall shape of the body. The body shape determines the wake characteristics—but that doens't mean the mechanism by which the pressure becomes lower in a 'bad' wake can't be the 'jet pump'.
I disagree with Duell and George that the main effect of the shear layer is to pull air into the wake. I agree with their general depiction of vortexes in the shear layer. I think my mental model here is something like this:
Shear layer vortexes entrain air from both the high speed flow and from the wake.
It's probably even true these vortexes entrain more high speed flow than they do wake flow. But because the total mass of available high speed flow is so high, and the total mass of the air in the wake is so low, the overall effect "feels like" pulling air out of the wake.
D+G are right of course that vortexes are then "shed" from the wake. Although they don't say it explicitly as far as I could see in their paper, I suspect that some vortexes are also "absorbed" by the wake—upstream air needs to enter the near wake, not just enter the shear layer.
So then if shear pulls air out of the wake, what brings new air into the wake? In terms of an "actual mechanism", as I said in the last essay, I admit that the shear layer also brings new air into the wake—after all, the wake is surrounded on all sides by shear layer. There's nowhere else for the air to come from. But in terms of wake mental models, it's much more fruitful to think of pressure as being what draws air into the wake.
In other words, the stronger the shear forces pulling air out of the wake, the lower the pressure will become to encourage new air to enter the wake.
Sources of replacement air
Second, it's useful to think about how air will get into the wake to replenish the air lost through shear forces. When a wake is "trapped" on all sides by high-speed airflow1, the pressures in the wake will be lower. Think of the rear-view mirrors on a semi truck or the small wake trapped on the rear windshield of the high-drag Ahmed body.
These wakes can only replenish themselves by drawing in fast-moving air, so the pressure has to be quite low in order to influence that air in the short time it's moving past the wake.
The rear wake behind a car or heavy truck, however, has much more moderate pressures. And if we look at the flow field, we see that the turbulent, slow-moving air passing through the underbody is usually the air the ends up in the wake. This air spends more time crossing through the wake's pressure gradient, and so is more "easily" drawn into the wake than the high-speed airflow above the car.
A 2017 paper by Castelain et al ("Identification of flow classes in the wake of a simplified truck model depending on the underbody velocity") shows that there's a such thing as the velocity being too low, as well. I think this paper comes as close as anything I've found to touching on the topics I've been writing about in these essays. So let's dig in on it a little bit.
Castelain et al rigged up a simplified truck model so they could control exactly how much airflow traveled through the underbody to the rear of the truck during wind tunnel tests.
They found something of a U-shaped curve when they plotted the relationship between underbody flow rate and surface pressure/drag (on the tail end of the vehicle).
If there's high-speed flow coming from the underbody, the drag is high as the wake has no source of low-speed flow and must make the pressures even lower to draw in that high-speed air. The wake is surrounded on all four sides by strong shear layers.
When the underbody flow is moderate, the drag is lower—this is the case we see in many real-world cars and trucks. There's a 'sweet spot' where the wake can get "just the right amount" of replacement flow, so the pressure doesn't have to 'work too hard' to encourage more air in.
But if the underbody flow is too low, the drag will once again be high. Zero airflow from the underbody ends up being identical to high-speed underbody airflow—the only "sources" the wake has are all high speed flow2—the wake can't get enough air from the underbody so the pressure drops to encourage more high-speed flow to become entrained. (At least, that is my interpretation of their results.)
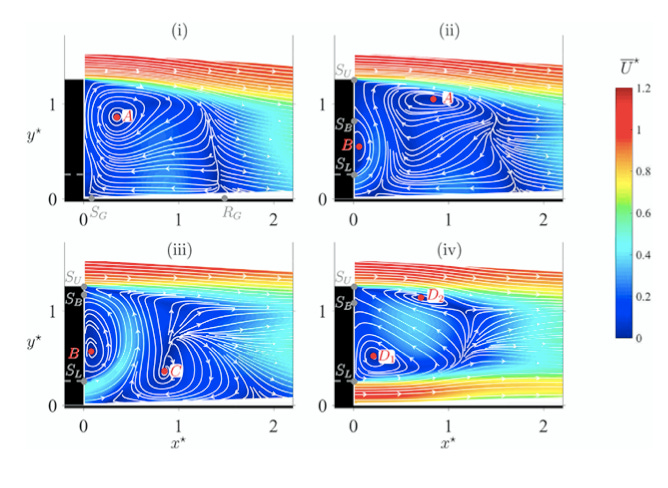
In the image below that I've reproduced from Castelain, the graph is measuring surface pressure on the back of the vehicle—so lower pressure (lower on the graph's y-axis) means more drag. The region labeled (I) corresponds to "not enough" underbody flow, (II) corresponds to "right amount of underbody flow", while (III) & (IV) are "too much" underbody flow.

I'm not sure why the drag in (III) is higher than in region (IV). I admit that doesn't seem to match the basic version of my shear-vs-pressure story. My best guess here: while I think the story I'm laying out here is generally true, there are certainly other factors as well—and the wake of underbody flow region (III) happens to fit correspond to a better wake shape along some parameter that's not captured by my mental models.
Castelain et al have this to say:
For class (III)...., a new clockwise recirculation bubble appears near the ground, whose center C is axially located between SG and RG. The existence, behind the base, of a vortex whose vertical size is around H, with strong curvature and velocities, potentially induces large low pressure values in the direction of B. Due to the proximity of B, the base is therefore largely contaminated by these low pressure values for class (III),
In other words, they're—at least sort of—engaging in the same sort of thinking we've seen before: "the vortex core is close to the surface, so the pressures are bad". But if you look at region (II), which had the best performance, there's a vortex core close to the surface, too. And region (IV), which has significantly better pressures than (III), is hardly further from the surface.
I started off by saying wakes (and aerodynamics in general) are strange and chaotic, and I think that's the best I can say here, too. I don't really know what's going on here—a phrase aerodynamicists should all get better at using.
Thinking in terms of impulse
Third, building on the previous discussion, I find it useful to think about "impulse"—a concept from high school physics class— for determining how air will enter the wake. Impulse is basically a momentum change due to a force acting over time. Imagine a particle of air near the edge of the wake, in a region where it has some chance of either being drawn into the wake or not. As the particle flows past the wake, it's subject to some pressure gradient, delta-p. How much will that pressure gradient affect the particle's direction of motion? Well, that depends on how much time the particle spends in the pressure gradient. The force acting on a particle multiplied by the time that force is acting is the impulse.
Thinking in terms of impulse helps us understand why wakes preferentially draw in lower speed flow. High speed airflow (coming from above the roof, for example) is moving much faster, so it's subjected to the wake's pressure gradient for a shorter period of time. The impulse—the change in the particle's momentum—is lower. Air moving at a lower speed will be subject to the pressure gradient for a longer time, meaning the total momentum change drawing it towards the wake will be greater.

Of course, these two sources of airflow are present on different parts of the wake, so there's no guarantee that they're subject to the same pressure gradient. But the wake is curved, so we know there must be some pressure gradient on all sides. And I think the fact we do see airflow entering the wake from the underbody tells me this is a basically correct way to think about it.
Impulse can also help understand why the pressure is lower when a wake is totally surrounded by strong shear layers (aka surrounded by high speed flow). Up to now, I've said that the pressure is lower because more air is pulled out by the stronger shear forces. Another way to think about it is that the pressure is lower because the time an air particle spends on the edge of the wake is lower, so pressure must be lower to impart enough momentum to draw some of those particles into the wake. (I'm not sure if one of these two models is "more true", or whether they're two sides of the same coin.)
But if pressure is balanced against momentum (stronger pressure gradients—lower pressures—are needed to draw in faster moving particles) then why does it matter whether shear forces pull particles out of the wake?
Well, if no air was leaving the wake—if it was truly a "dead water" zone, then there would be no need for any of this. The pressure wouldn't need to change based on impulse, because the wake would 'feel' no need to draw air into itself. It's only because something is drawing air out of the wake that the wake has a need to draw more air in. And the "something" pulling air out of the wake certainly isn't the pressure field—the curvature of the wake is proof enough of that.
Ideal gas law/Conservation of mass considerations
Another tool I've used to think about wakes, that I still can't decide whether it's truly useful or not, is the ideal gas law. As we've seen, wakes are generally "fed" by a source of low-speed flow. They have a volume defined by the edge of the wake. If you can make that volume smaller, while the wake is still being fed by the same amount of upstream flow, you should see the pressure rise. The Ideal Gas Law says that for a given amount of matter (and temperature of the gas), the pressure-times-volume is constant. So, decrease the volume and the pressure will rise to compensate.
Do I think the Ideal Gas law actually applies to wakes? Of course not. With all the mixing & flowing that takes place in the wake, obviously the assumptions under which the law is true will be broken. But it can be useful as an aspect of your intuition. Roughly speaking, lower pressure means "less air"—it's 'harder' for air to get in, so pressure drops to encourage it. And when the same source fills a smaller volume of air, the pressure will increase. But as we've certainly seen many times by now, this is just one factor of many, and often, a smaller wake means more drag.
Conservation of mass has similarly felt useful for staying "grounded" in thinking about wakes. As with the Ideal Gas Law, conservation of mass doesn't *literally* apply. However, in the long term, the mass of the wake isn't changing over time. For any flow that enters the wake, and equivalent mass will eventually be drawn out of it; and when more air mass than "average" is drawn out of the wake, the pressure will drop to draw in fresh air.
Pressure recovery (in the far wake); closing the wake
"Pressure recovery", as I've seen & heard it used, is a term used to discuss the pressure downstream of the wake. In other words, behind the wake, how quickly—how far downstream—does the pressure "recover" from its low pressure in the wake back to a neutral pressure? I've heard this referred to as the "far wake"—it's not a recirculation region, so maybe not a wake in the strict sense, but it is "in the wake" of the car, to use the term in the less strict sense someone on the street might.
When we use the term "pressure recovery", we're not thinking about the size of the wake specifically, but rather thinking about getting the far downstream areas to have a pressure closer to "normal" air.
At first, when I'd hear people say one design had "better pressure recovery" than another, I assumed this idea was either (a) tautologically obvious or (b) meaningless words because we don't know what actually made the design better.
But I later came to decide that it could be a useful concept, even though I sort of still think those points are true, too. Here's why I like it—it basically boils down to a similar "pressure gradient" argument like I made in the "impulse" section, just this time applied in the direction the vehicle is traveling:
We know that when air reaches the "free stagnation point" of the wake, it could either start moving downstream, or be drawn back into the wake.
That air is experiencing some pressure gradient in the x-direction (the upstream-downstream direction)—the particle 'feels' a pressure gradient, but the absolute pressure doesn't matter
So say a pressure gradient of [X] Cp/m is "required" by the wake to draw in enough air to stay constant. Any increase in the pressure downstream of the wake means the pressure in the wake can rise by the same amount without affecting the pressure gradient.
In other words, the higher the pressure is downstream of the wake, the less likely it is to see the "popping off" of shear layer vortexes described by Duell and George, because there's a pressure gradient fighting against it. (This is far from the only factor in this wake popping, probably not even one of the most important factors. But logically it should be *a* factor.)

I have mixed feelings about using the (far wake) "pressure recovery" concept when discussing wakes. On the one hand: I like that it's a valid concept, in the sense that I can draw a diagram of how it works. On the other hand: I don't think it's a concept I can reliably use to design better cars—I still don't know how I would have any control over the far wake, in contrast to how boat tails, for example, interact directly with the shear layer.
I also used to hear the term "closing the wake" a lot. While it sort of refers to similar concepts, I like this term even less. From what I've seen, aerodynamicists mostly use it as an equivalent to "the wake got smaller" when discussing the differences between two designs. But, as we've seen before, the wake getting smaller is not consistently associated with better drag, so "closing the wake" shouldn't be our goal unless we're aware of an underlying reason why a smaller wake would help this particular design.
Wrapping it all up
I think of wakes as a balance between forces of shear (pulling air out of the wake) and pressure (drawing air into the wake).
Small wakes are not always better; big wakes are not always worse.
Unlike some previous aerodynamicists—but not all—I believe that it's useful and basically true to think of shear forces as pulling air out of the wake, not entraining air into the wake.
Bluff body wakes seem to be "best" (in terms of the amount of drag they cause on a vehicle) when they have a source of air that can be drawn into the wake "easily". In other words, somewhat slower-moving air. In real cars and trucks, this comes from the underbody.
(This is not true for more aerodynamic shapes like airfoils, which have such a small wake they don't really need to worry about replenishing air.)
Thinking about impulse (a force applied over time) helps us understand why this is the case—the total momentum imparted to an air particle on the edge of a wake is greater when that particle spends more time subject to the wake's pressure gradient.
Pressure recovery (downstream of the wake) is helpful—a higher pressure downstream of the wake allows for a higher pressure in the wake without changing the x-direction pressure gradient. However, I'm not sure there's a way to use this idea in practice.
There are other factors besides the ones I've focused on here that influence the characteristics of a wake. Some of them are known and some of them, I expect, are still not fully understood. Even as we understand wakes better and better, the best we can say will still often be "I'm not exactly sure what's going on here".
I don't think my evidence is as convincing as it could be if we ran some tests/simulations specifically meant to test these ideas. I'd like to help make that happen someday (or find them if they've already been published).
McLean pointed out that the characteristics of a wake are basically determined by the shape of the body that's upstream of it. And I agree with him, but I've tried to advance our understanding by providing a convincing description of the mechanics by which a body's shape turns flow characteristics into surface pressures in a wake (more streamlined body—> stronger shear layers at bluff body edges—>more air pulled out of the wake—> lower pressure). But if the drag is determined by the body, what's the point of all this? I guess I'd say a few things:
A better understanding of these mechanics can help us predict the effects of design changes upstream—for example, we know we want a source of "not too fast" airflow for the wake to draw from.
Better understanding these mechanics may help with design in the wake area, as well. I haven't thought too deeply about applications here, but the obvious example is that the "shear pulls air out" theory argues in favor of using more boat tail-style designs.
Perhaps having a clearer view of these mechanics will help us someday understand wakes in a way that allows us to better control them, (somewhat) independently of the upstream object's shape.
Thanks for reading & feedback is extremely welcome.
References
Castelain, Thomas, et al. "Identification of flow classes in the wake of a simplified truck model depending on the underbody velocity." Journal of Wind Engineering and Industrial Aerodynamics 175 (2018): 352-363.
Plus whichever side(s) of the wake touch the vehicle surface
Just this time, it's on three sides instead of four