All posts in this series:
1. Aerodynamics is beautiful and strange. Wakes especially so
2. A not-short-enough introduction to wakes and drag
3. Big wakes and small wakes
4. How should we think about shear layers?
5. My mental model of wakes
Let's really start our investigation of ground vehicle wakes with a simple question: to make a design more aerodynamic, do you want the wake to be bigger or smaller?
Perhaps some of the aerodynamicists reading this will think the answer is too obvious to be of interest. But in my opinion, the complexity it will take to answer this question is a great way to start thinking more carefully about the aerodynamics of wakes.
Let's jump right in.
Make it streamlined?
Why do I say that some readers might think this question is too simple to be of use? Perhaps even those of you who know next-to-nothing about aerodynamics could come up with the first answer we'll discuss to the question of wake size.
Do you want the wake to be bigger or smaller? Well, streamlined shapes (like airplane wings) have low drag and they also have small wakes. Un-streamlined shapes have high drag and big wakes.
For example, Figure 1 below is a diagram I found online of the drag coefficient of different shapes. The drag coefficient is a number that quantifies how much drag an object creates. A lower drag coefficient is better (less drag means it cuts through the air more efficiently):
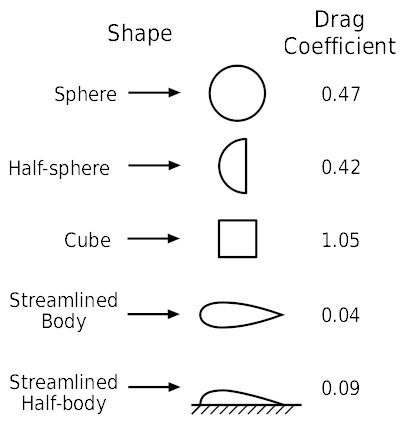
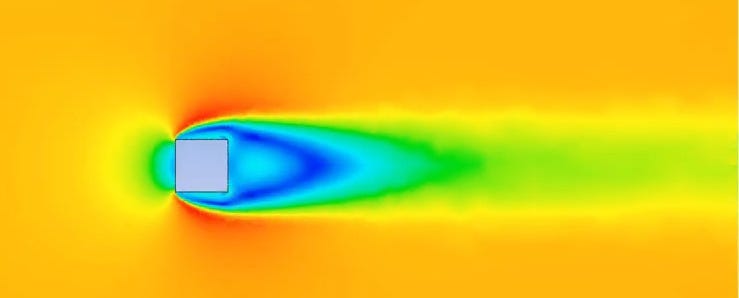
A cube has a drag coefficient of 1.05. It also has a very large wake, as you can see in the image below:
An airplane wing—an airfoil—(referred to as "streamlined body" in the chart above) has a drag coefficient in the range of 0.04, ~25x less than that of the cube.1 Its wake is also much slimmer, as you can see below:
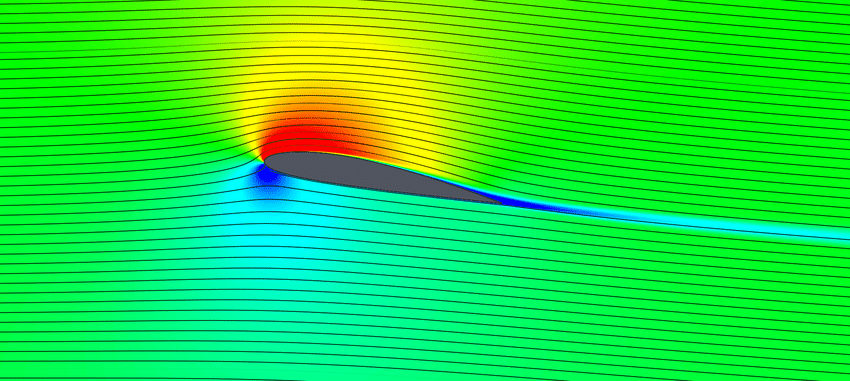
In the two images above the objects are stationary and the air is moving from left to right—the same convention used in the images in previous posts. The two images are showing slightly different visualizations, but for both of them we can say that the blue colored region 'behind' (i.e. to the right of) each object represents the wake.2 The cube's wake is bigger than the cube itself, while the airfoil's wake is nearly nonexistent.
So, in short, there's some truth to this answer. We can say for sure that very streamlined (i.e. low drag) objects have small wakes, and that very un-streamlined, high drag, objects have large wakes. But—as we'll soon see—that's not the same thing as saying "on this particular car, if we make the wake 1% smaller, we'll also make the drag 1% lower".
"Streamlined objects have smaller wakes" is an important part of the answer to our question. It's a strong starting point, but it's not where the discussion ends.
Vortex centers and infinitely long wakes?
Warning: we're going to really start getting into the weeds now. While there's a basic understanding that smaller wakes are better, it's actually not hard at all to find examples where larger wakes show up together with less drag.
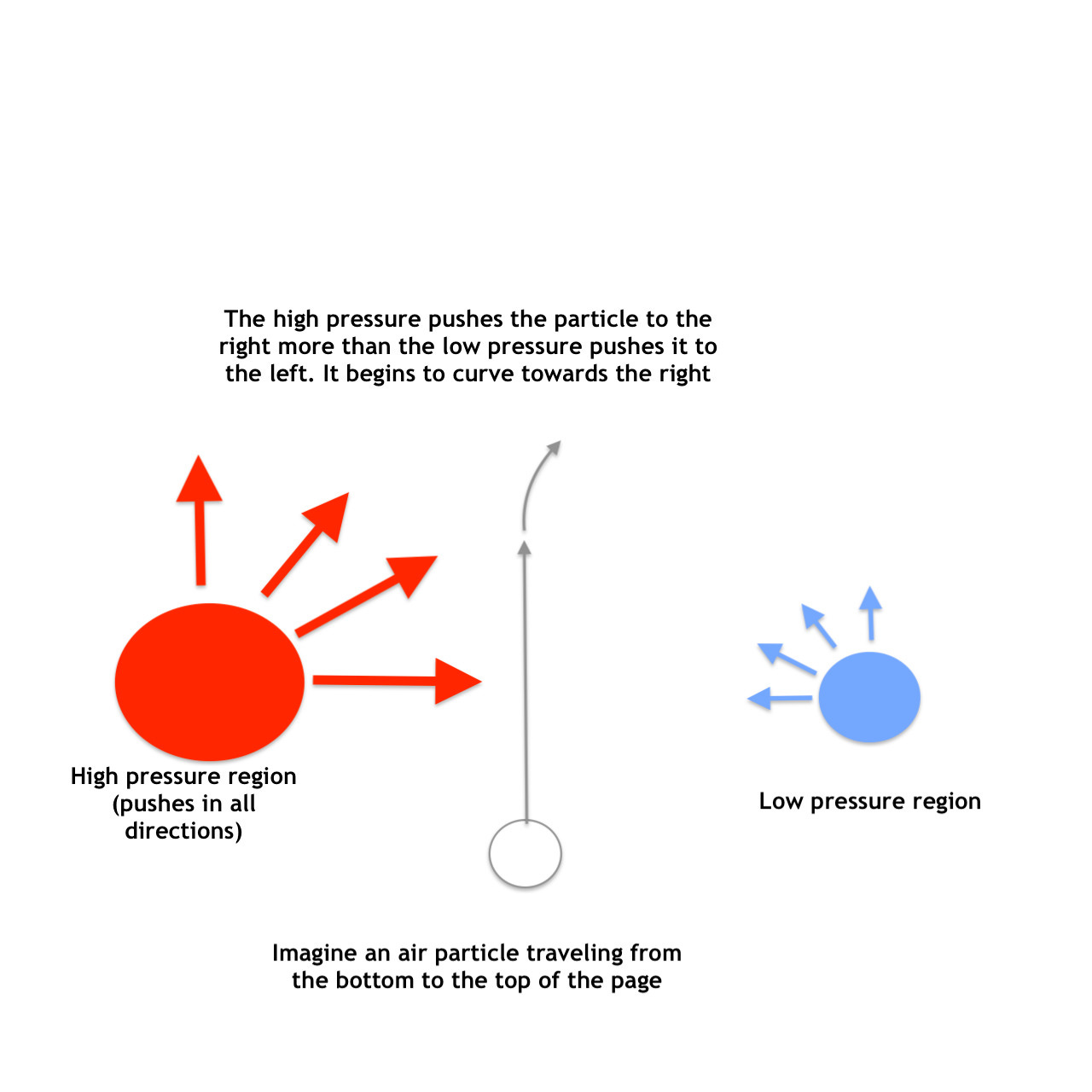
One way aerodynamicists often try to rationalize this is by talking about the vortex core of the wake. Let’s get an understanding of why people think this way. First, remember, from our discussion of drag, how the only thing that truly matters for drag is the pressure of the fluid that's touching the car's surface? That's point number one in this argument. Then combine that with point number two: Moving air always curves towards a region of lower pressure (we'll see why below). As a result, the center of a vortex will always have the lowest pressure in the region of that vortex.
Even non-experts may be familiar with the fact that a vortex’s lowest pressure is at the center: you may have heard that the central 'eye' of a hurricane has low pressure—and you may have noticed the air spiraling around that eye is always curving towards it (though never reaching it).
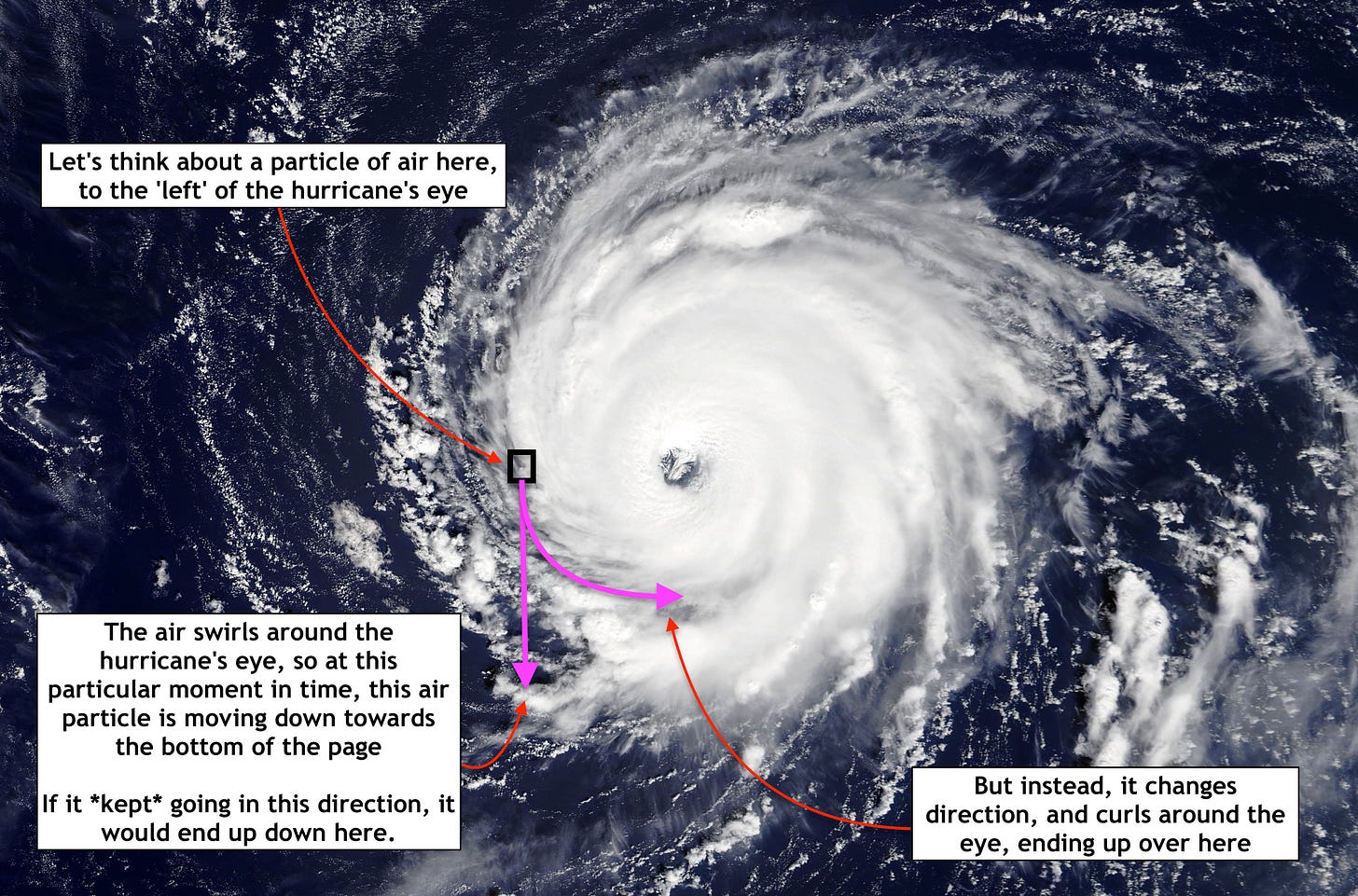
Here's why air behaves that way: imagine a particle of air, moving through a region where there's relatively higher pressure on one side, and relatively lower pressure on the other side. In Figure 5 below, the air is moving from bottom to top, and the high pressure is on the left. That higher pressure pushes the air away from it with more force than the low pressure on the opposite side resists it. The air that was once moving in a straight line will curve to the right—towards the lower pressure:
By extending this line of thinking we can prove that for any region where the flow is curving—whether a hurricane, a tornado, or the wake behind a car—the lowest pressure is at the center of the vortex.
OK, so why does all this matter? Well, some aerodynamicists have engaged in a like of thinking that goes something like:
Hey, we know that drag is due only to the air contacting the *surface* of the car
And, we know that the lowest pressure in a vortex happens in the vortex's 'core'
So, if we move the core—that region of lowest pressure—*further from the surface*, we'll have less drag on the car...right?
For example, in a 2019 paper titled "Vehicle Aerodynamic Optimization: On a Combination of Adjoint Method and Efficient Global Optimization Algorithm", the authors state:
Figure 11 shows the comparison of wake flow region between the baseline and the optimized model... It is clear that a large-scale vortex is formed in the wake region behind the spoiler and rear window of each model. The vortex of the optimized model stays farther away from the rear window compared with the baseline model, which might be one of the contributions to the higher pressure on the rear surface of the optimized model...
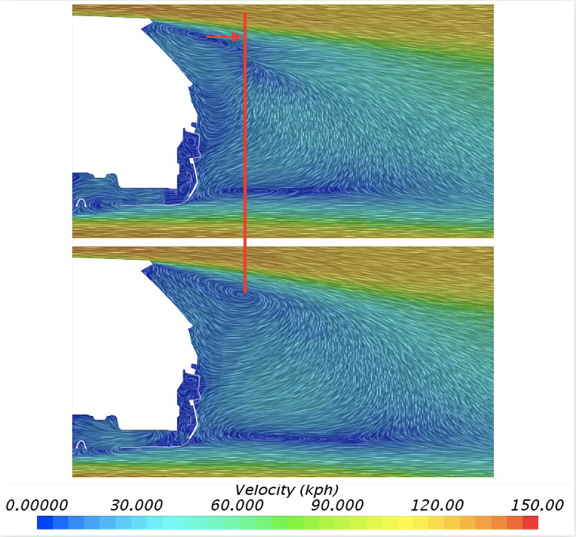
Example #2: in a 1999 paper titled "Experimental Study of a Ground Vehicle Body Unsteady Near Wake", authors Duell and George first report on another author's earlier work, saying:
Kruiswyk and Dutton investigated the effect of cavities on a two dimensional body and determined that the shed vortices are formed slightly downstream of the trailing edge of the cavity. By displacing the vortex formation away from the model base, the low pressure of the vortex center is not communicated to the base, thus raising the base pressure between 10 to 14 percent. [note from me: "base pressure" means 'the pressure (and thus the drag) on the back end of the car'] 3
They later say of their own results:
The effects of base cavities on the unsteady pressure in the near wake were investigated. The mean base pressure increases with increasing cavity depth 11% higher than the base case model. The unsteady near wake is shifted downstream and the recirculation length is increased when the cavity is in place.
The base cavity they are mentioning in these quotes is a set of panels attached to the end of the "model". A real-life example is the "boat tail" you may have seen on the back of some semi trucks if you've driven on US highways:

For a final example, we’ve previously seen an image of what I called a "donut vortex" from Tadatsu et al. in previous posts. Being some sort of aerodynamics sicko, I actually have a (early?) version of this paper with a different abstract from the abstract in the paper I see online. The abstract on my version says:
This paper describes a relationship between aerodynamic drag on vehicle's backward face and the vortices behind the vehicle. The result shows that the further vehicle backward vortices exist from vehicle's backward face, the lower aerodynamics drag on vehicle's backward face becomes.

So, is this a good way to think about wakes? In my opinion, no—this "move the vortex further from surface" line of thinking is bad aerodynamic analysis.
Why? Well first of all, it doesn't pass a sanity check. If moving the vortex further from the surface is good, then moving it further and further would be better and better. But that obviously can't be true—it would imply we want an infinitely long wake behind the vehicle. (Why would that be bad? Here's one of the few places where I think it's useful to use the "car driving down road" reference frame instead of the "stationary car in wind tunnel" reference frame: an infinitely long wake would mean the car is pulling an infinite amount of air down the road behind it.)
The other problem with this explanation is that it doesn't account for the possibility of other changes to the flow field. Yes, the vortex core moved further away, and yes, the lowest pressures are in the vortex core, but there's no guarantee that the changes which led to the core moving further away didn't also lead to a different pressure in that vortex core. We can't just say "vortex core further away = good", because anything that changes one part of the flow field (the location of the core) has the potential to change every part of the flow field (e.g. the pressure in that core, the pressure gradient between the core and the surface, etc).
But let's get back to what really matters here—the fact remains all these authors found better aerodynamic performance in vehicles with longer wakes.
So, clearly we can't simply say "smaller wakes = good". But for the reasons discussed above, we can't just say "bigger wakes = good", either. Where does that leave us? How should we be thinking about wakes?
The Ahmed body phenomenon
Let's look at one more example, which doesn’t fall into the same “move the vortex further away” category of thinking, and which is possibly the most interesting phenomenon in all of car aerodynamics.
In 1984, S.R. Ahmed and his co-authors developed a simplified car model to use in their studies. It's now known as the 'Ahmed body', as in the title of this section.
(The term "body" is used here in the same sense we use the phrase "bluff bodies", discussed previously. However, if you do an image search for "Ahmed body", you will unfortunately sometimes see images of guys named Ahmed showing off their body. But I digress.)
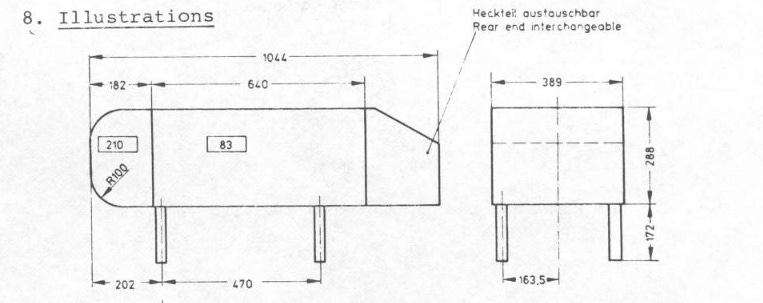
Their model is extremely simplified—it's a rectangular block with a few curves in the front and a slant in the back to represent the rear windshield. Here's a diagram from the original paper:
And here's a more modern, 3D picture from a flow simulation:

Ahmed et al. found something extremely interesting when studying this model. If you look closely at the blueprint above—Figure 9—you'll see they note that the "rear-end [is] interchangeable". They ran wind tunnel tests with a variety of different angles for the slant of the rear windshield. What they found is that at a certain angle—30°—the model could have two different drag values.
For some tests, the drag coefficient would be 0.378. In other tests, it would be much lower, at 0.260. If you ran the wind tunnel for 60 seconds, the drag might be low (.260) for thirty seconds, and then suddenly switch to being high-drag (.378) for the next thirty seconds.4 And this is not a small difference—it's roughly a 30% change.
I'm not quite sure how to properly convey how unexpected this is. As you may remember from high school, one of the basic tenets of science is "if you run the same experiment again, you'll get the same results". In aerodynamics, we mostly hold true to that tenet as well—the "drag of simple bodies" chart above didn't have to explain "oh, sometimes the square has a drag coefficient of 1.05, but at other times the drag coefficient is 1.42". 99.99% of the time, the drag is just the drag. But strangely, this one car could have two different drag values.
Perhaps you can guess how this finding connects back to the main theme of this essay—the low-drag flow field of this Ahmed body has a larger wake, and the high-drag flow field has a smaller wake.
Here's a picture of the low-drag flow field from a 2021 paper by Liu et al.:
And here's a picture of the high-drag flow field from a 2015 paper by Zhang et al (Zhang is also one of the co-authors of Liu's 2021 paper, but not the same Zhang mentioned in the last section, as far as I can tell):
I'm being not as careful here as I could be. While the "bistability" occurs at 30deg, the "high drag" paper investigated a 25deg windshield slant angle, and the low drag paper investigated a 35deg slant angle. However, I think aero engineers will agree these results are still representative of the flow fields for the two drag values at the 30deg angle itself.
So what matters in these pictures? Note how the "high-drag flow field"—Figure 12—doesn't even include the entire slanted 'windshield'. That's because the flow is mostly still following the path of the model's surface. Here's a 3-D diagram of the high drag Ahmed body flow field:
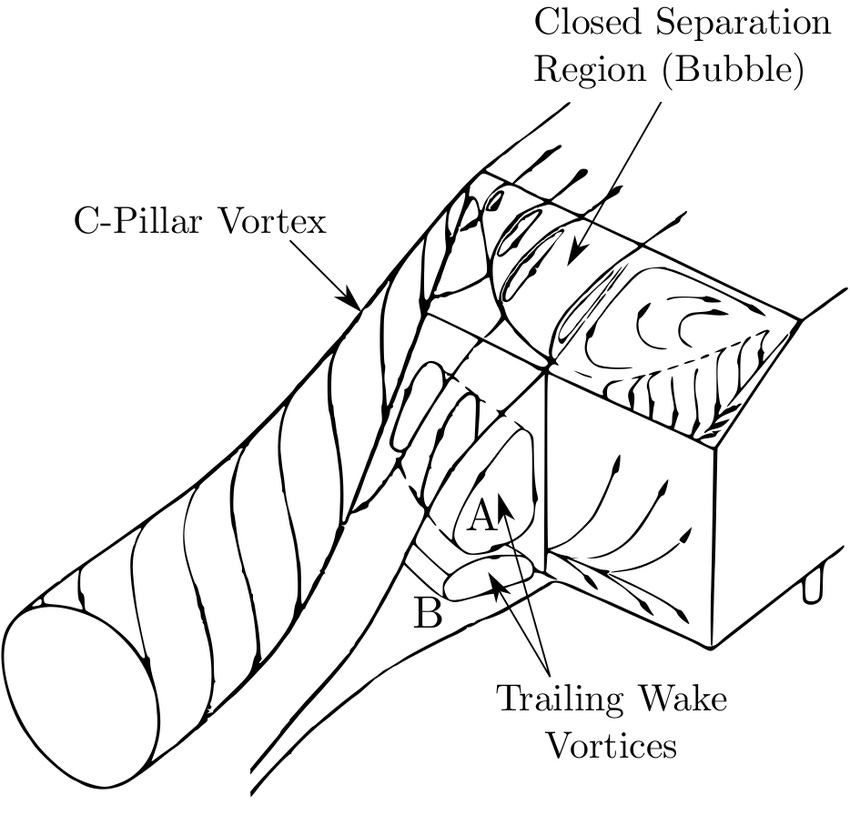
Note how in the low drag flow field, the rear windshield is fully enclosed in the wake. But when the drag is high, there's a tiny wake that's "trapped" on the upper part of the windshield (Labeled "Closed Separation Region (Bubble)" in Figure 13 above). This wake is quite small...and it also adds lots of drag to the car. Contrary to our original cube-vs-airfoil example, the much larger wake in the low drag flow field creates much less drag. I can say that with confidence because we have the surface pressure data which tells us which parts of the car are adding to the drag.
For example, in a 2017 paper titled "On multistabilities of real car's wake", authors Bonnavion et al. included an image of surface pressure measurements for a real car (a Renault) that experienced a very similar phenomenon.
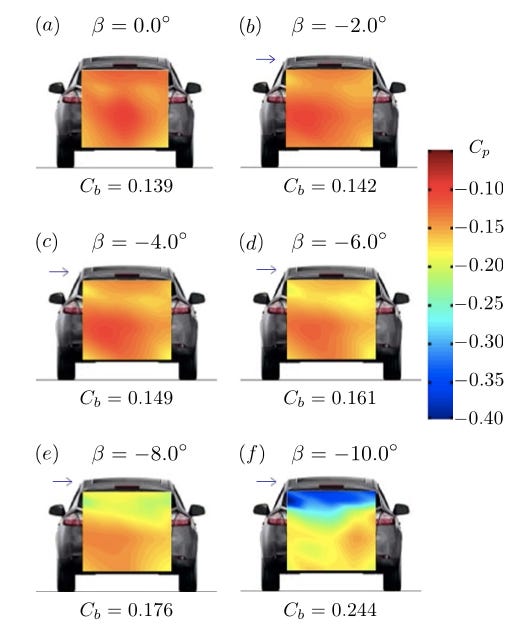
Above I've reproduced Figure 9 from Bonnavion et al (now Figure 14 in this essay). Note the bottom right vehicle—that's the "high drag" version of this car’s flow field5, and the extremely low pressures on the windshield are adding lots of drag. This wake on the rear windshield is small—much smaller than the wake that covers the rear windshield when the "low drag" flow field is present. But this smallness comes with extremely low pressures that add lots of drag6. Once again, we can't just say that smaller wakes are better.
(I've seen aerodynamicists focus on the "C-pillar vortex" (see Figure 13) as an explanation of why the drag is so high on the high drag Ahmed body. But in my opinion, this obviously can't be the case, because, as we've mentioned, only air on the car's surface contributes to drag. The C-pillar vortex travels downstream and only touches a small bit of the rear windshield, and thus only has a small direct contribution to drag.)
Conclusion
Hopefully you're convinced by now that aerodynamics isn't as simple as saying "smaller wakes = bettter". Yes, extremely streamlined objects have small wakes and low drag, while extremely unstreamlined objects have large wakes and high drag. But when we look at semi-streamlined 'in-between' objects, like cars, and especially when we make comparisons between similar cars, we can't just measure the length of the wake to determine which is more aerodynamic.
Aerodynamicists will often come up with some rationalization for why bigger wakes are sometimes better, even though everyone “knows” smaller wakes are better. At least in the papers I’ve seen, authors never seem to notice what they’re doing—if a smaller wake means less drag, they have one explanation, and when a bigger wake means less drag, they have another explanation, without ever stopping to think, hey, this is weird…
We need a more nuanced way of understanding what makes a wake good or bad.
References:
Ahmed, Syed R., G. Ramm, and Gunter Faltin. "Some salient features of the time-averaged ground vehicle wake." SAE transactions (1984): 473-503.
Bonnavion, G., et al. "On multistabilities of real car's wake." Journal of Wind Engineering and Industrial Aerodynamics 164 (2017): 22-33.
Liu, K., et al. "Flow structure around a low-drag Ahmed body." Journal of Fluid Mechanics 913 (2021): A21.
Tadatsu, Masaya, et al. "A Study on Aerodynamic Drag Reduction for Two-Box Car." Transactions of Society of Automotive Engineers of Japan 44.5 (2013). (Japanese: "2Box 車の空気抵抗低減に関する研究")
Zhang, Yang, et al. "Vehicle aerodynamic optimization: on a combination of adjoint method and efficient global optimization algorithm." SAE International Journal of Passenger Cars-Mechanical Systems 12.06-12-02-0011 (2019): 139-153.
Zhang, B. F., Y. Zhou, and Suet To. "Unsteady flow structures around a high-drag Ahmed body." Journal of Fluid Mechanics 777 (2015): 291-326.
Obviously this will change somewhat based on the shape of that particular airfoil. The airfoil in the flow image isn't the same shape as the one in the "drag of simple shapes" diagram and so probably has a slightly different drag coefficient, but the general point is true.
The cube is showing the velocity field, while the colors on the airfoil image are showing the pressure field. But wakes tend to have both low velocity and low pressure, so that’s not a big deal for our current purposes of just pointing out the vastly different wake size.
If I understand correctly, Duell and George are making a slightly different point than Zhang et al. are making in the first example, but I don't think it's worth going into the details here.
I've already mentioned that the flow field is ever-changing. Since the drag on a car is based on its flow field, you may not be surprised to hear that the drag is ever-changing, as well. So when we talk about a car having one (or in this case two) drag value, that value is assumed to be an average over some amount of time. The low-drag Ahmed body has a drag value that oscillates chaotically above and below the low-drag average value; the high-drag version has a drag value that oscillates continually around the high-drag average value.
Details that I’m leaving out: unlike the original Ahmed body which tested different windshield angles, the “bistability” of this car appears only when there’s a certain amount of crosswind. The six images show the surface pressure of the same car when experiencing different amounts of crosswind.
Remember: low pressure = vacuum = drag because it’s pulling the car backwards