How should we think about shear layers?
Do they pull air into or out of a wake?
All posts in this series:
1. Aerodynamics is beautiful and strange. Wakes especially so
2. A not-short-enough introduction to wakes and drag
3. Big wakes and small wakes
4. How should we think about shear layers?
5. My mental model of wakes
We learned in the previous essay that we can't simply use "small wake = good" as a heuristic for understanding wakes. What will we use instead? I'll do my best to answer that question in next essay, but first we need to talk about another feature of wakes that I think mainstream aerodynamics often gets wrong: shear layers.
To recap our introduction to shear layers from an earlier post, we know a few basic things about them:
First, a shear layer is our name for where high-speed and low-speed flows meet on the edge of a wake:
Second, shear is basically friction. To quote my earlier essay:
The 'shear' in shear layer comes from the concept of shear stress. I think of shear stress as being basically like friction. Take one hand and rub it back and forth across your other forearm. Because of friction, your hand will pull the skin of your forearm slightly in the direction your hand is moving. The skin on your forearm, likewise, is pulling your hand against the direction it wants to move, making it slightly harder to move your hand.
Something similar happens to fluids like air. When a high speed flow interacts with a nearby low speed flow, the high speed air will "pull on" the low speed air, causing it to speed up a bit. The low speed air, likewise, will equally "pull against" the high speed air, slowing it down slightly.
And third, because of this friction, the shear layer is full of mini vortexes. They don't show up in a time-averaged image, like Figure 1 above, but the transient flow field looks something like this:

Here's a YouTube video that shows how those mini vortexes combine and grow as they move downstream. Although there's no "car" in this video, the basic set-up of the flow is similar to Figure 1 above: flow is moving left-to-right, high speed flow on top, lower speed flow below, like the situation at the edge of the rear roof in Figure 1:
(I also just wanted to include this video because it was posted to YouTube by Clinton Winant, a researcher who published an influential 1974 paper showing how the vortices in a shear layer combine as they flow downstream. Pretty cool to be studying shear layer vortexes in 1974 and keep doing it for so long that you end up posting shear layer vortex videos on YouTube!)
To recap, here's the basics of shear layers:
A shear layer is our name for where high- and low- speed flows meet on the edge of a wake.
Shear is something like friction in the air—high-speed air pulls on low speed air, speeding it up. Likewise, low speed air pulls on high speed air, slowing it down.
The shear layer is full of small swirling vortices, which combine together (growing larger) the further they are from the rear edge of the car.
With that background, let's start to try understand how we should—and shouldn't—think about shear layers, and how they relate to the rest of the wake.
What I don't like about Duell & George
Duell and George's paper has clearly been influential—the image we just saw above is reproduced in Aerodynamics of Road Vehicles, a textbook which is widely considered to be the "car aerodynamics bible". I agree the paper does a very good job of describing the shear layer vortex structure. However, their paper leaves me wanting in a few places.
I believe, basically, that D+G are wrong about how the shear layer relates to air entering and exiting the wake. I realize as I write this that I haven't really said much previously about air entering or exiting wakes, and why that might matter, so let's take a quick detour:
Remember that what we "care about" as designers is the air pressure directly on the surface of the car. I've described wakes previously as a (slight) "vacuum", and that term can help our intuitions here—roughly speaking, the less air there is in a wake, the more of a vacuum it is (i.e. the lower pressure it is). That vacuum pulls the car backwards, adding to the drag of the car1. We'll get into this more below and in the next article, but basically: there is always air entering and leaving the wake, and while this can get complicated, to some extent, we want air to be able to get into the wake—a lack of air, after all, is vacuum. What I'm going to be arguing in this article is that we need to think more carefully about how air gets into and leaves the wake.
So, in short: we care about air getting into the wake. And in my opinion, Duell and George don't really explain how. D+G say fluid is "entrained into the near wake through the shear layers". I think that statement is less convincing than it seems. Look again at their diagram:
Yes, upstream high-speed air coming from along the sides of the model gets entrained into the shear layer. But the shear layer is, at least in their diagram, distinct from the wake itself. The near wake (in their terminology) is what contains the air that actually touches the base of the model.
D+G later mention that vortexes are "shed at the free stagnation point" (as shown in the bottom half of Figure 2 above)2. Do all shear layer vortexes get shed downstream when they reach the free stagnation point? Or are some of them absorbed back into the wake? They only mention vortexes being shed. While there's a description of how free stream air gets entrained into the shear layer, there's no explicit description of how shear layer air would then enter the near wake.
Unless there's a quote from their paper that I missed, when we put it together there's not actually any explanation of air entering the wake. High-speed air is entrained into shear layer vortexes, but those vortexes are then shed from the end of the wake. There's air entering the shear layer, and there's air exiting the shear layer at the tail end of the wake, but there's no actual description of air entering the (non-shear-layer) wake. And that really leaves us wanting, because it's the "near wake", not the shear layers, that comprise the vast majority of the fluid that actually touches a car's surface.
Before I make my attempt to explain where air is entering and exiting the wake, let's first take a look at another analysis of wake/free-stream interaction that, in my opinion, also gets things wrong.
The 'jet pump' fallacy?
Understanding Aerodynamics: Arguing from the Real Physics, by Doug McLean, was once suggested to me as the best textbook on aerodynamics. And I do like it a lot! But I think McLean mis-understands wakes, as well.
In section 6.1.7, he argues against thinking of the wake as a "jet pump mechanism"— in other words, he argues against the idea that the shear layer "mixes with the dead air and tries to pump it away". So, while D+G said the shear layer brings air into the wake, McLean is going to argue something similar—that it doesn't pull air away from the wake. I think they're wrong. McLean doesn't call it a "fallacy" himself, but the header section refers to it as a "questionable drag category". This is what he says:
Hoerner (1965) [...] proposes that “base drag”3 is determined by a “jet-pump mechanism,” which is supposed to work as follows (paraphrased):
The “jet” is the outer flow, “placed like a tube around the space behind the base,” and it “mixes with the dead air and tries to pump it away,” thus reducing the base pressure. The separated boundary layer has an “insulating” effect that reduces the effectiveness of the jet pump. The longer the forebody, the thicker will be the boundary layer that separates from the edge of the base and the less effective the jet-pump mechanism will be in reducing the base pressure..."
The problem with Hoerner's explanation is that it ignores the dominant role of the outer inviscid flow in determining the pressures on the body. The separated shear layer that forms the outer boundary of the near wake can support very little pressure difference across it, so the base pressure must be essentially the same as the static pressure in the inviscid flow outside the boundary layer where it separates from the edge of the base. This static pressure is a result of the external inviscid flow, as influenced by the effective displacement shape of the forebody and the separated wake downstream. The thickness of the boundary layer at separation influences the effective shape of the wake to some extent, but the static pressure at separation, and thus on the base, is much more strongly driven by the overall shape and fineness ratio of the body, through the inviscid flow. So the correlation of the “base drag” with forebody fineness ratio is much more of an inviscid-flow effect than a result of any “jet-pump mechanism.”
Figure 4 below is an image from Hoerner's book, which McLean refers to in a sentence I didn't include in this quote. The vertical axis (y-axis) is the drag on the rear of the projectile—the "base". The horizontal axis (x-axis) is the drag on the front part of the object—the "forebody" as he calls it. The shape of the curve shows us that when the forebody drag is very low, the base drag is very high (the top left portion of the graphed data). When the forebody drag is much higher, the drag on the base is relatively low (the bottom right data points).
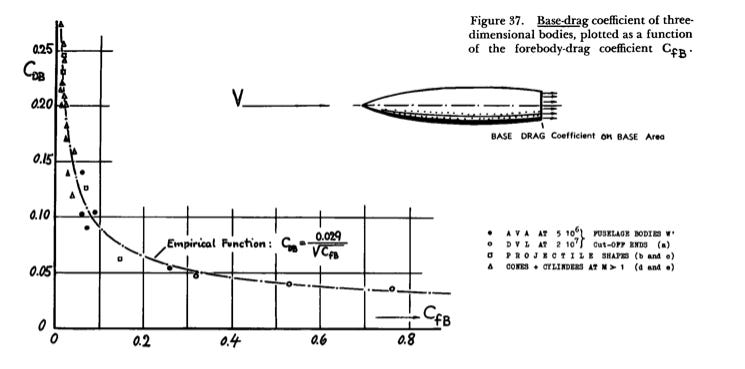
Results like this are well-known in aerodynamics, and are commonly seen when designing cars and trucks. Make a small design change to the front of the vehicle, and the drag in that local area will go down, as we expected it to. But often an increase in the drag on the rear of the vehicle offsets most, if not all, of those localized aerodynamic improvements.
McLean is familiar with this phenomenon. However, he disagrees with the "jet pump" hypothesis as an explanation. He says, "the static pressure at separation, and thus on the base...is much more strongly driven by the overall shape...of the body". Now, on the one hand, I partly agree with him. The drag on an object is determined by its shape. An airfoil has much lower drag than a cube. And that shape is going to be mostly upstream of the wake—by the time the air gets to the wake, the drag has basically already been determined.
But for someone who wants to really understand wakes, this statement isn't very useful. It's nearly tautological—bodies with better shapes are better. Well, yes, but how so? What's different about the wakes in those bodies?
So while I partly agree with McLean, in a much more important way, I disagree with MacLean's argument here. Although I don't quite have slam-dunk proof, I think it's clear that shear layers pull air out of the wake—in other words, I think the "jet pump" effect is real, not a fallacy. In my opinion, it's one of the few truths we have that allow us to think accurately about wakes and how they relate to the drag on cars and trucks. McLean's right that the flow field is determined by the body shape, but, in my opinion, he's wrong when he says that means the jet pump mechanism doesn't exist.
By saying this, I'm also disagreeing with Duell and George. While they aren't directly dealing with any 'jet pump'-type arguments, they state clearly that the shear layer is where air is entrained into the wake, not where air is pulled from the wake. I've already explained how I think this phrase isn't an accurate summary of their own findings. I agree that air is entrained into shear layer vortexes. But it's not clear that's the same thing as air being entrained into the near wake. (They themselves admit those vortexes are later shed from the wake.)
So now we've seen two sources, over the course of roughly fifteen years, one of which claims that the shear layer draws air into the wake, another that makes a slightly different claim, that the shear layer doesn't pull air out of the wake.
I think both are wrong. Let's starting finding out why I think that way.4
Where do we see the lowest pressures?
Let's start with a little quiz. Below are two images of aero simulation results, both showing (from the rear view) the surface pressure of a vehicle—one car and one semi truck. The two color scales are not identical and shouldn't be compared directly, but in both cases they run from dark blue (lowest pressures) through green (neutral pressure) to dark red (highest pressures).
Our quiz question is: where do we see the lowest surface pressures? (Footnote: Remember: Low pressure on a surface that faces backwards is bad for drag—it's a vacuum pulling the car backwards.)
First, here's the surface pressure pattern typical of an SUV-style car (somewhat overly zoomed in, sorry):

And here is a typical image of the surface pressure on a semi truck:
So where are we seeing those lowest pressures that add the most drag (per square inch)? It's a bit of a trick question, because those lowest pressures aren't on the back of the vehicle at all—it's the surface of the rearview mirrors that has the lowest pressure—much lower than the "base" of the car/truck.
Could we have predicted this by theorizing about wakes? I say yes—the mirrors, because there is not much 'vehicle' upstream of them, are exposed to "clean", high-speed airflow on all sides. This high-speed flow interacts with the dead air behind the mirror via the shear layers, and pulls it out, making the mirror's wake region into a stronger vacuum.
The actual rear end of the vehicle, as Figure 1 shows us, is generally exposed to high-speed airflow on three sides—but, and I think this is critical, the air coming from under the car has bounced around through the underbody and is at a much lower speed when it reaches the wake.
So if shear layers were what brings air into the wake, why would the mirrors, which are surrounded on all sides by strong shear layers, have a much stronger vacuum—i.e. much less air—than we see at the vehicle's rear, which has a much weaker shear layer on the underbody side?
Shear layers in the average flow pull air out by definition
Here's an interesting detail I've noticed about shear layers, that I think is *vastly* under-discussed in our understanding of shear layers. I'm not sure I've seen it discussed at all, in fact—as far as I know, it's something I just noticed by myself at some point. I may have read it somewhere, but if I did, it was so long ago that I have no idea what the source is.
That detail: In the *average* flow field, air can ONLY be pulled out of the wake by shear forces, and is NEVER pulled in.
While that may sound extreme, it's not a wild claim—in fact, I'd argue it's a simple mathematical certainty. Let me prove it to you.
First, we need to know that shear forces, by definition, act parallel to the direction of a particle's motion. To return to our metaphor of rubbing your hand against your other forearm: the friction will pull the skin on your forearm sideways, but it won't be pulled up towards your hand nor pushed away from it.
Second, wakes, by definition, are always a concave shape. I use concave in the sense of the definition provided by my computer's dictionary app, "having a surface that curves inward like the interior of a circle". We already saw previously that flow will always circulate around the region of lowest pressure. Wakes are no exception—they curl around the region of lowest pressure (the donut-shaped vortex core we've seen before). Because of that, the edge of the wake is always curved slightly inward, like a circle (it's not a coincidence that wakes are sometimes called "recirculation regions").
At the edge of the wake, we can think of there being two shear effects, as discussed before:
High speed air "pulls" on low speed air and speeds it up a bit
Low speed air "pulls" on high speed air, slowing it down a bit (in the exact opposite direction)
But here's the key: shear stress happens parallel to the direction of motion, and on the edge of a concave curve, tangent lines never point inside the curve. The shear stress vector of that first effect (high speed pulling on low speed) is pulling air downstream out of the wake. But the 2nd shear stress vector (low speed pulling on high speed) DOES NOT point in the direction of pulling air into the wake. It slows the air down, yes, but pulls in a direction that would still leave it outside the wake. Here it is as a diagram:
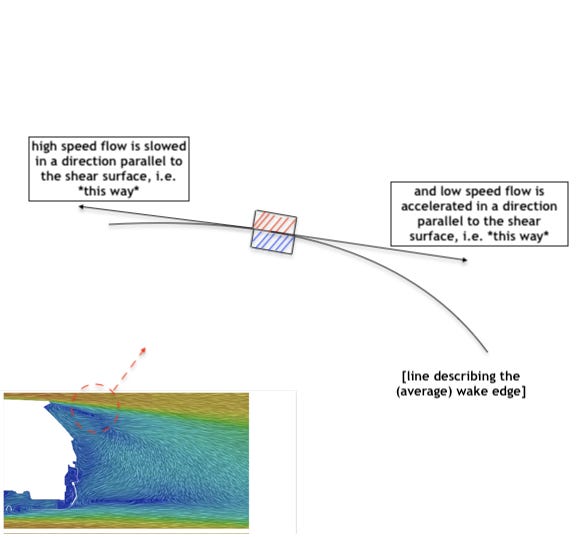
Note how neither of those arrows—representing the force vector of the shear stresses—point inside the curve representing the wake's edge. Again, I admit that this is only true of the time-averaged flow. In the true, transient flow field, the existence of shear layer vortexes means that shear stresses are pulling air in different directions at different moments. But I find it hard to believe that transient shear layers pull air into the wake given that the averaged shear layers are pulling air out of wakes.
Because I can only say this about the averaged flow, it's certainly not indisputable proof, but I find it convincing enough that I think the pressure should be on those who believe the shear layer entrains air into the wake to prove that entrainment is actually happening.
Boat tails and shear layers
Let's look at one more example that's influenced my intuition on shear layers: boat tails. I've already said a little about "boat tail" devices sometimes used on the back of tractor-trailer trucks . As a reminder, here's a representative example of what they look like:
In my opinion, understanding that the jet pump fallacy isn't a fallacy—that high speed flow pulls air away from the wake—is the key to being able to understand why a boat tail is so effective. And they are quite effective—a boat tail like the one in the image above could improve the drag coefficient by 10% or more (see quotes in the previous article from Duell & George paper).
From a perspective of "the shear layer rips air out of the wake", it's easy to understand why boat tails work: by separating the high speed flow from the low speed flow, it's much harder for the high-speed flow to rip air out of the wake, especially near the surface of the vehicle, which is where the drag actually happens, as you know by now.
The "air enters the wake through the shear layer" perspective makes it difficult to understand why a boat tail would work. If the shear layer is putting air into the wake, then blocking that air from entering the wake shouldn't make the pressure in the wake higher. A wake, like a balloon, should see its pressure rise when air enters it, not when air is prevented from entering.
This confusion perhaps explains the claims we saw in the previous essay that boat tails work because they move the low-pressure vortex core further from the surface of the vehicle—if you believe the shear layer entrains air into the wake, you need to come up with some convoluted explanation for why boat tails are effective. But, as I explained in the last post, I believe that line of thinking is obviously poor aerodynamic analysis, and the truth is much simpler: shear layers rip air out of the wake, and boat tails stop that from happening.
(Though with all that said, I’m still having some second thoughts here. Boat tails don’t stop the shear layer from existing, they just move it further downstream. Perhaps there’s something to be said for not ripping air out of the wake near the vehicle’s surface.)
So, how *does* the air enter the wake?
So if air (mostly) doesn't enter the wake through the shear layers, how does it enter the wake? Well, I've already sort of discussed my answer to this question: for things that are shaped like real-world cars and trucks, it seems like flow enters the wake through the underbody. I'll get into this more in the next article, but more generally, you might say that air enters the wake via the air source that it's easiest for the wake to draw air in from—and that's low speed flow, not high speed flow.
A couple caveats here:
First: in a way, I'm not really disputing the "enters through the shear layer" hypothesis. The air coming from the underbody, while slower than free-stream air above the car, is generally moving faster than the air in the wake. So there's still a shear layer between the underbody air and the wake. It's just not as strong.
The fact that air preferentially enters the wake through certain shear layers is, in my opinion, an important nuance that helps us have a much more useful mental model of wakes. In other words, what D+G say is true, but to the extent it's true, it's tautological—the wake is surrounded by shear layer, and air enters the wake, so of course it enters through the shear layer. If that's all we can say, it doesn't help us understand wakes much better.
Second: obviously this argument can only apply to these car- and truck-like shapes that do have a weaker flow in some area (generally underbody). Obviously for something like a bullet (as in Hoerner's data, Figure 4 above) there's a strong shear layer on all sides—and air must be entering the wake through the strong shear layer. But as Hoerner points out, those bodies have very high rear drag—air coming into the wake through a strong shear layer isn't exactly a good sign.5
When we look at images of the average flow field, it usually appears that air is coming into the wake from the underbody:
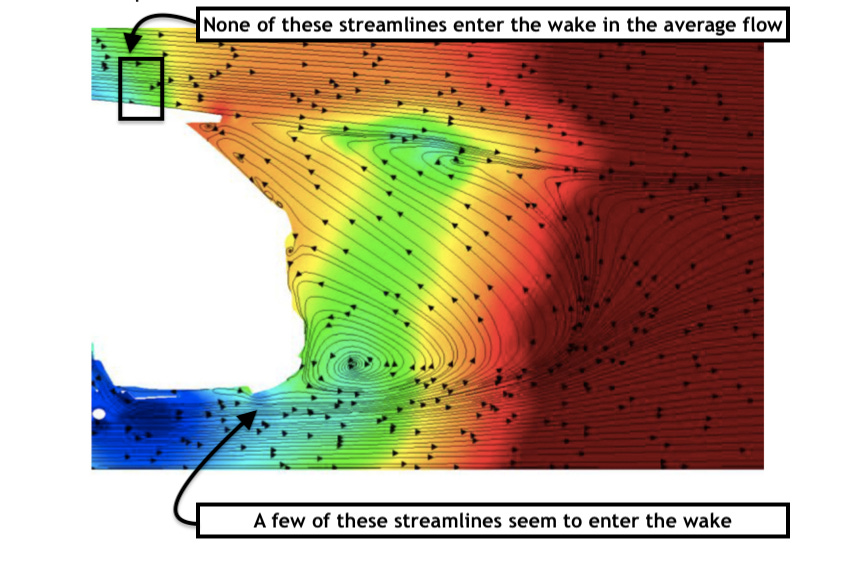
Again, this is a time-averaged flow field, so it's tough to say for sure whether the time averaging is revealing the truth or obscuring the truth. I tend to believe it reveals the truth. Even I don't think Figure 9 is particularly compelling, but let's look at one more similar argument for wake airflow coming from the underbody.
Rear windshield soiling
Soiling is the study of how small non-air particles (water droplets, dust, etc) interact with a moving vehicle and its flow field. Visibility on the road can become a dangerous issue if the windows become covered with dust or rain, so car companies run soiling studies to design components with shapes that minimize the possibility of these issues. And we know from soiling studies—both simulations and real-world tests—that dust and water droplets in the rear underbody end up deposited on the rear windshield.

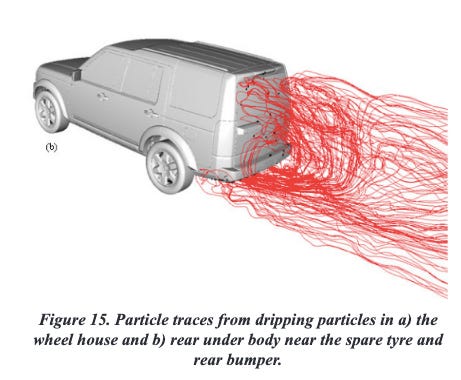
It's perhaps worth pointing out that these particles must be traveling along with the air— since they're heavier than air, they wouldn't float up from the underbody if they weren't being borne upwards on the air.
This is, once again, not quite as convincing proof as I'd like to have here. We have solid proof that there's air in the wake that's coming from the underbody. But on the other hand, that certainly doesn't prove that there isn't also some air entering the wake from the higher-speed shear layers above.
D+G said that air is entrained into the wake via the shear layers. To me, that might imply that more/stronger shear means more air entrained into the wake. But rather, it seems that air is coming into the wake through the weakest shear layers, and Hoerner is right that stronger shear layers show up together with stronger vacuum pressures—i.e. a lack of air in the wake.
Conclusion
To recap:
McLean argues that shear layers don't pull air out of the wake. Duell and George go a step farther, arguing that shear layers pull (entrain) air into the wake.
I think they're both wrong (with the caveats discussed above), and that Hoerner had it right all the way back in 1958—shear layers pull air out of the wake.
There are a few pieces of evidence that lead me to this conclusion:
As shown by Hoerner—Figure 4 above—and in my example of the strongest vacuum pressures happening on the rearview mirrors (which also have the strongest shear layers)6, stronger shear consistently correlates with higher drag.
It's a mathematical fact that in the time-averaged flow field, shear stresses only pull air out of the wake, not into it.
"Shear pulls air out of the wake" gives us a simple story for why boat tails work, which lets us avoid imprecise explanations about moving the vortex core further downstream.
As best I can tell, air mostly enters the wake through the underbody of a typical car—when given the opportunity, air enters the wake where the shear layer is weak, not where it's strong.
While I'm pretty convinced that we shouldn't think of shear layers as entraining air into the wake, and while I hope I've made some points that argue effectively for that conclusion, I admit we don't yet have the type of proof we could have if we chose to study this more thoroughly. I'd love to see some experiments/simulations designed to give confirmation or disproof of these ideas (or perhaps those experiments have already been run in the 6 years it's taken me to turn this idea into a published essay...).
These past two articles have been somewhat disjointed—while connected by the theme of "things I think other aerodynamicists have gotten wrong", they don't do the best job of explaining what I do think is true about wakes. That's where we'll go next.
References
Dasarathan, D., A. Farag, and M. Ellis. "CFD Comparison with Wind-Tunnel for a Class 8 Tractor-Trailer." The Best of COMVEC 2016 Select Technical Papers from the SAE Commercial Vehicle Engineering Congress. SAE International, 2016.
Duell, Edward G., and A. R. George. "Experimental study of a ground vehicle body unsteady near wake." SAE transactions (1999): 1589-1602.
Gaylard, Adrian Philip, and Bradley Duncan. "Simulation of rear glass and body side vehicle soiling by road sprays." SAE International Journal of Passenger Cars-Mechanical Systems 4.2011-01-0173 (2011): 184-196.
Hoerner, Sighard F. "Fluid-dynamic drag." CHAPTER V-Drag of Surface Imperfections (1958).
McLean, Doug. Understanding aerodynamics: arguing from the real physics. John Wiley & Sons, 2012.
Schuetz, Thomas Christian. Aerodynamics of road vehicles. Sae International, 2015.
Sun, Shaoyun, et al. "Aerodynamic shape optimization of an SUV in early development stage using a response surface method." SAE International Journal of Passenger Cars-Mechanical Systems 7.2014-01-2445 (2014): 1252-1263.
Winant, Clinton D., and Fred K. Browand. "Vortex pairing: the mechanism of turbulent mixing-layer growth at moderate Reynolds number." Journal of Fluid Mechanics 63.2 (1974): 237-255.
Zhang, Yang, et al. "Vehicle aerodynamic optimization: on a combination of adjoint method and efficient global optimization algorithm." SAE International Journal of Passenger Cars-Mechanical Systems 12.06-12-02-0011 (2019): 139-153.
And of course, it pulls in every direction—it also pulls on the air outside of the vacuum, so to speak
I don't disagree with this point
Remember that a "base" just means the flat-ish back end of a car-like shape
MacLean makes a comment in the quote above that I've never been able to understand. He says: " The separated shear layer that forms the outer boundary of the near wake can support very little pressure difference across it...". This is the very first sentence of his counter-argument, and so it seems to be an important part of what he's arguing, but I'm not really sure what he means. This is the only time I can ever remember reading about the ability of a certain region of the flow field to "support"—or not support—a pressure difference. Is he just saying that the pressure can't change rapidly over a short distance, here or anywhere else in a flow field? I wish I understood this comment better.
Some of the more aerodynamic modern cars are also beginning to have quite streamlined underbodies. But these vehicles also tend to curve smoothly back together at the rear end, unlike the very bluff back of a bullet, so the situation isn't quite so dire
Shear stress is stronger when the velocity difference is stronger




(as a pilot) Your point made in the diagram in Figure 7 about tangent of the shear layer friction always pointing outside the curve, is that how venturis and bernoulli's principle work?
I'll be looking through your posts to see if there's an explanation for vortex generators too, which always seem like magic to me. Cool posts!